Area of an Isosceles Triangle and Online Tools

A Triangle contains Two Equal Sides.

Triangles are basic shapes in geometry. Meanwhile, one special type is the isosceles triangle. An isosceles triangle isn’t your everyday triangle. Its specialty is that it has two sides that are the same length. It is not an ordinary shape. To find the area of an isosceles triangle, you must rely on the simple formula, Area= ½ x Basex Height.

Area of an Isosceles Right Triangle Properties:

Equal Side Lengths

The most distinguishing feature of an isosceles triangle is its two sides being of equal length. This symmetry opens up a world of possibilities in geometric calculations.

Base Angles

In addition to equal side lengths, isosceles triangles have equal base angles. Understanding these angles is crucial for further exploration of their properties.

Area of a Right Isosceles Triangle Formula:

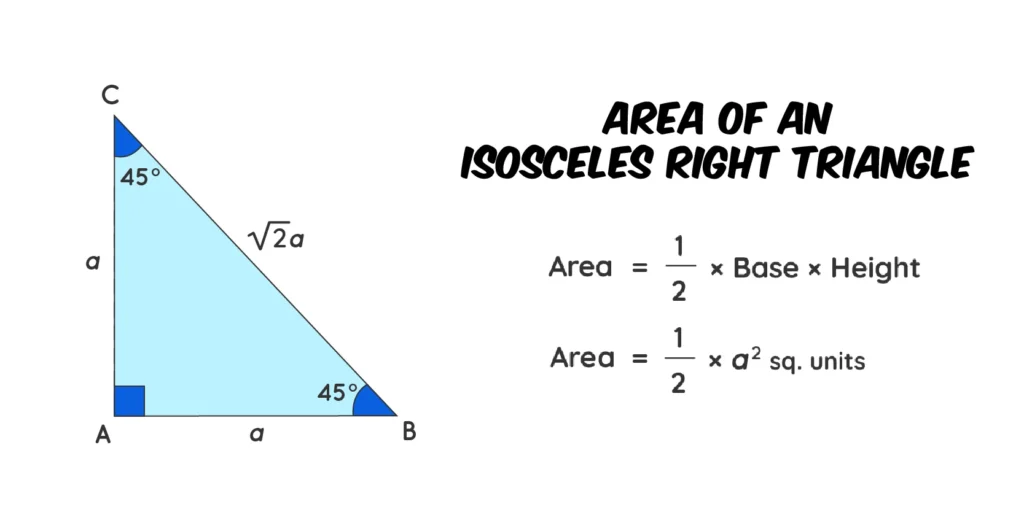
Apply the following formula for the right isosceles triangle. 

Area: B x H x 0.5

H: Height distance from the base to the opposite vertex. 

B: Represents the length of the unequal side.

Practical Example of the Area of a Right Isosceles Triangle:

Follow the Following example to understand the formula practically.

1. An isosceles triangle with a base of 8 units and a height of 6.
2. Add these values into the formula:

Area: 0.5 x 6 x 4 = 12

Uses of the area of an Isosceles Triangle

The area of an isosceles triangle is a small piece of geometry knowledge. However, it holds the following significance importance.

Architectural Preferences:

Architects often deal with structures that incorporate isosceles triangles. Knowing how to calculate the area ensures accurate planning and design, contributing to the stability and aesthetics of buildings.

Engineering Applications:

Whether working on bridges or machinery, you must encounter isosceles triangles in various forms. 

Also, it helps you calculate the correct area for optimizing materials and ensuring the structural integrity of components.

Design Aesthetics:

Visual appeal is a prominent factor in fields like graphic design or art. Therefore, understanding the area of an isosceles triangle aids in creating balanced and aesthetically pleasing compositions.

Mathematical Foundations:

To make a strong foundation in maths, you must Learn about isosceles triangles and their area in geometry. This knowledge becomes a building block for more complex mathematical concepts. Also, it gives you a solid base for further studies.

Problem Solver:

Whether you are measuring a space for furniture or crafting DIY projects, this knowledge has practical applications.

Educational Significance:

Remember, Understanding the area of geometric shapes is a crucial aspect of mathematical education. 

Effectively dealing with isosceles triangles boosts confidence and encourages a deeper appreciation for the beauty of mathematics.

Efficient Resource Management:

The area of an isosceles triangle helps you with inefficient resource management. In fields like agriculture or land surveying, efficient land use is crucial. Therefore, the ability to calculate the area of irregularly shaped plots, often containing isosceles triangles, aids in resource management.

Real-world Problem Solving:

Isosceles triangles Help unexpectedly in real-life scenarios. From designing a banner for an event to calculating material requirements for a DIY project, the Isosceles triangle is present for you. Meanwhile, The ability to compute their area allows for effective problem-solving.

Spatial Awareness:

Understanding isosceles triangles and their area contributes to spatial awareness. This skill is valuable in mathematical contexts and day-to-day tasks that require a sense of space and dimension.

Enhanced Critical Thinking:

Critical thinking is essential for growth and productivity. Therefore, Engaging with the properties and area calculation of isosceles triangles enhances critical thinking skills. It encourages individuals to approach problems methodically and think logically.

Tips for Calculating Area Efficiently

To efficiently calculate the area of an isosceles triangle, always use the  Area: B x H x 0.5 formula. And ensure that you correctly identify the base and height.

Common Mistakes to Avoid

Do not practice Common errors in calculating the area of isosceles triangles. It includes using incorrect side lengths or misidentifying the base and height. Always double-check your values.

Incorrect measurement:

One common mistake often is confusion about which side of the isosceles triangle is the base. 

Such a misunderstanding can lead to inaccuracies in the final area calculation. Therefore, It’s essential to be clear about the base identification. Also, ensure the accurate measurement of the perpendicular height for precise area computations.

Using wrong Side Lengths:

Using the wrong length for the base or sides can significantly impact the accuracy of the area calculation. It’s crucial to identify and input the side lengths into the formula correctly.

Wrong application of Formula:

Forgetting or misapplying the formula for the area of an isosceles triangle leads to wrong results. Sometimes, people apply formulas like the following.

• Area=12×Base×Height

It’s a common mistake. Understanding the relationship between the base and height is essential for accurate computations.

Ignoring the Equal Base Angles:

Since isosceles triangles have two equal base angles, neglecting this property might lead to height errors, affecting the overall area calculation.

Misinterpreting Side Lengths:

Assuming that all sides of an isosceles triangle are equal can result in using incorrect values in the formula. Remember that only two sides are equal in length in an isosceles triangle.

Using the Wrong Units:

Failing to use consistent units for the base and height can lead to dimensional inconsistencies in the final area calculation. Always ensure that the units match.

Rounding Errors:

Reducing intermediate values too early in the calculation process can introduce errors in the final result. 

It’s advisable to carry out calculations with sufficient decimal places before rounding.

Misunderstanding the Concept of Perpendicular Height:

Some individuals may need help with the concept of the perpendicular height. Because it leads to errors in measuring and applying this distance in the area formula.

Online Tools for Calculating the Area of an Isosceles Triangle:

In today’s digital era, several online tools help you to figure out the area of an isosceles triangle. Some of them are the following. 

CalculatorSoup – Isosceles Triangle Area Calculator:

CalculatorSoup offers a dedicated calculator for finding the area of an isosceles triangle. Users input the length of the equal sides and the length of the base, and the tool provides the calculated area.

Mathway – Isosceles Triangle Area Calculator:

Mathway is a versatile math tool that includes an isosceles triangle area calculator. Users can input the side lengths, and the tool calculates the area and provides step-by-step solutions.

Symbolab – Isosceles Triangle Area Calculator:

Symbolab offers an intuitive isosceles triangle area calculator. Users enter the known side lengths, and the tool instantly computes and displays the area.

Final Verdict:

Understanding the area of an isosceles triangle extends beyond the confines of a geometry classroom. Whether for academic purposes or real-world applications, this knowledge equips individuals to work with and analyze isosceles triangles effectively.